تقسیم ستاره در PCB به معنای رسم ترک (track) به یک شیوۀ ستاره مانند است. در رسم ترک ها در محیط رسم PCB اغلب اتفاق می افتد که بخواهیم یک ترک را به چند نقطه متصل کنیم. در رسم چنین ترکی معمولاً نوعی ترسیم استفاده می شود که به آن تقسیم ستاره می گوییم. تقسیم ستاره را در جاهای مختلف دیده ایم. مثلاً تقسیم ستاره در مقاومت ها یا انتقال برق سه فاز به موتورهای سه فاز به صورت مثلث یا ستاره. در PCB بحث تقسیم ستاره به معنای انشعاب گرفتن از یک ترک برای چند نقطه به صورت تقسیم ستاره است.
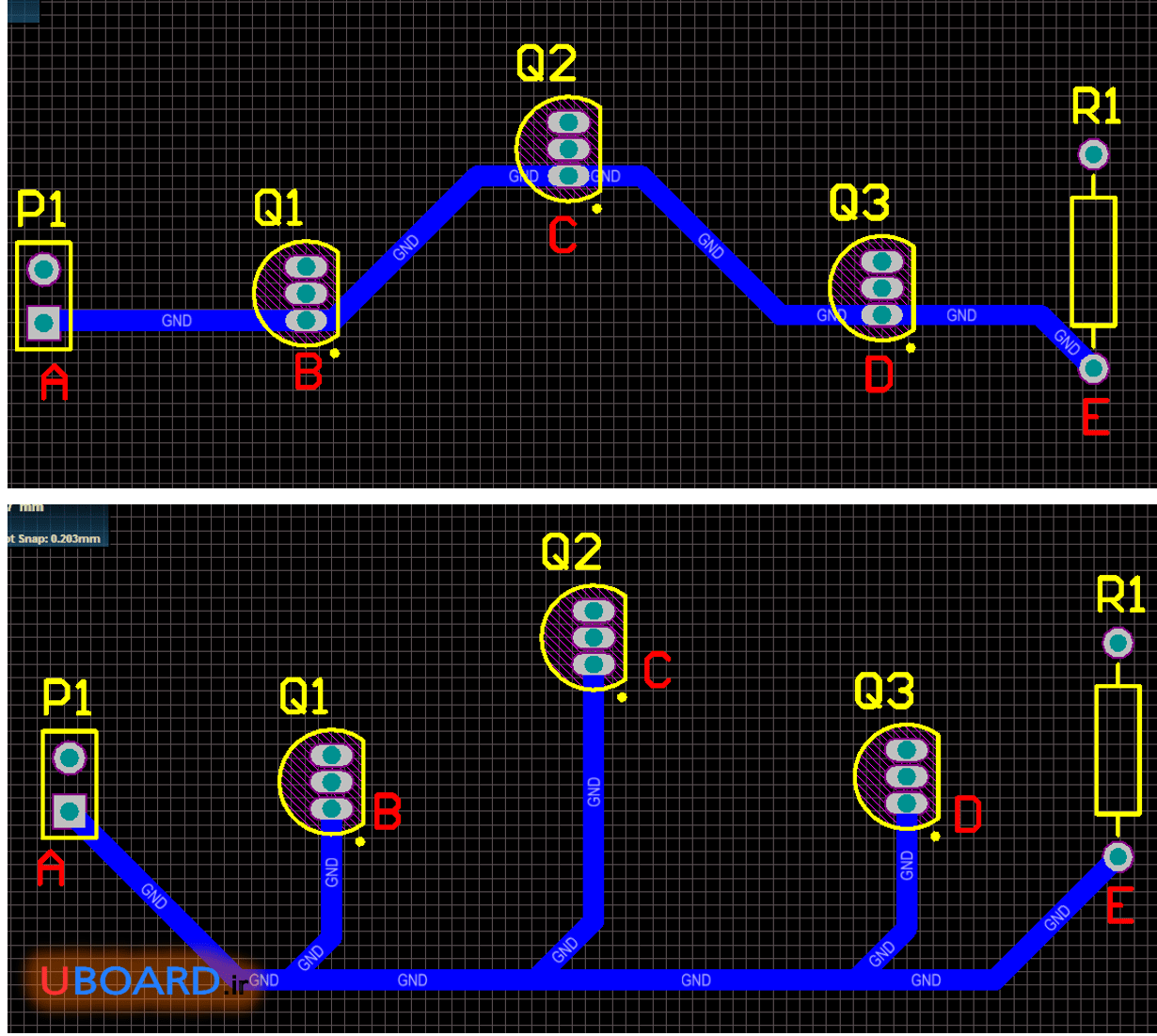
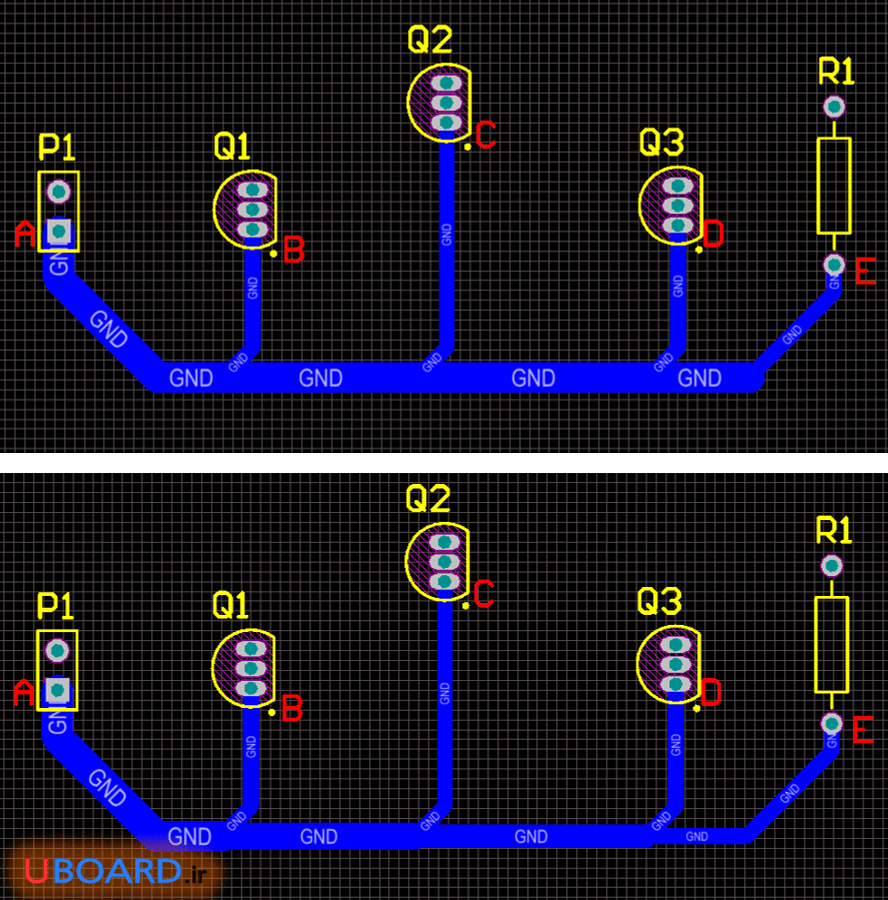
به تصویر زیر دقت کنید. می بینید که برای رساندن نقطۀ A به نقاط B و C و D و E از دو روش استفاده شده است. در روش بالا نت (net – گره) زمین از نقطۀ A ابتدا به B و سپس به ترتیب به C و D و E رسیده است. در واقع ترک از A به B، از B به C و … رسم شده است. در روش پایین ترک زمین از A به اخرین نقطه یعنی E وصل شده و در مسیر گذر آن، به نقاط دیگر انشعاب داده شده است. به روش دوم تقسیم ستاره می گویند.
تصویر 1 – روش تقسیم ستاره در رسم ترک (تصویر پایین)
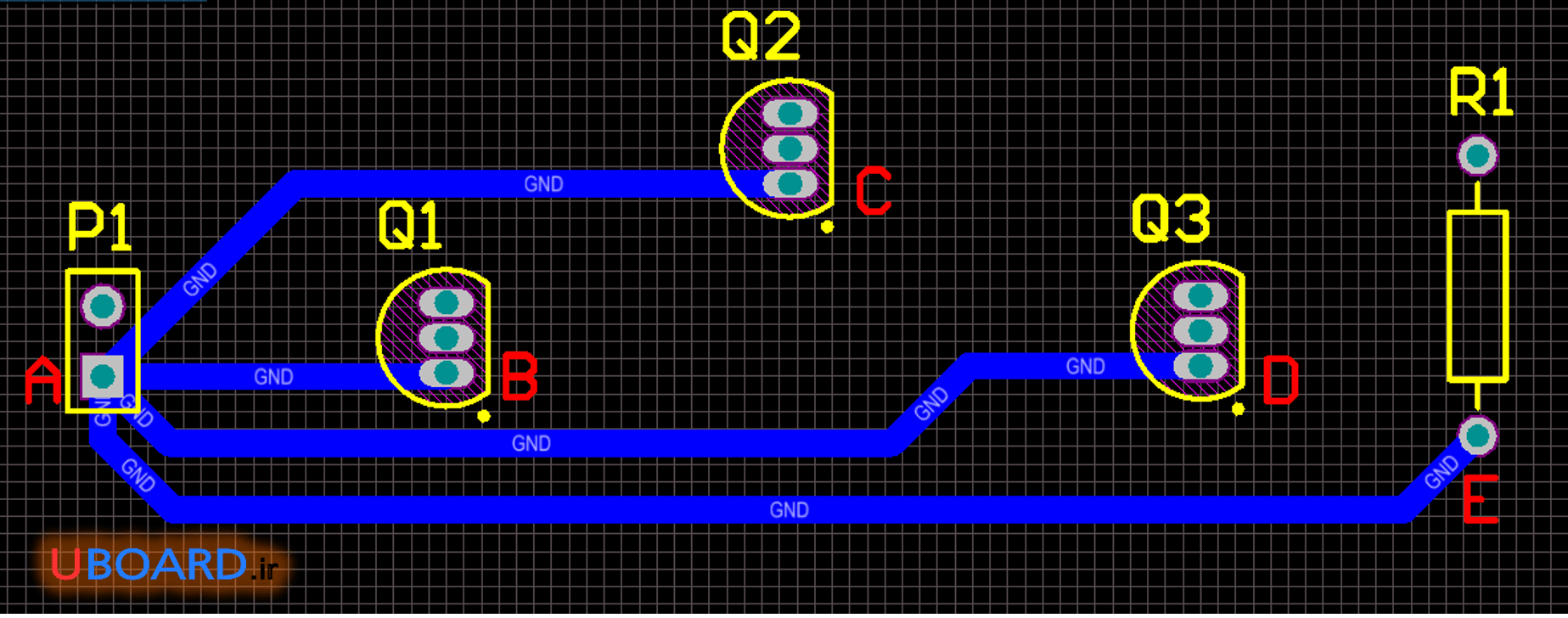
در هر دو روش زمین به نقاط B تا E رسیده است. شاید به نظر برسد تصویر بالا به دلیل مسیر ترک کوتاه تر بهتر باشد. اما اینگونه نیست. روش بالا به دلایلی که خواهیم گفت توصیه نمی شود. در روش پایین مجموع طول ترک ها بیشتر است. اما مزایایی دارد که روش بالا فاقد آنها است. تصویر زیر نیز یک نوع تقسیم ستاره را نشان می دهد. اما ما به دلیل این که این تقسیم ستاره فضای زیادی را از بورد می گیرد، از آن استفاده نمی کنیم. این نوع تقسیم ستاره ممکن است در PCBهای فرکانس بالا کاربرد داشته باشد. البته نکات طراحی PCB مدارات فرکانس بالا بسیار پیچیده تر و گسترده تر از بحث ماست.
تصویر 2 – نوعی تقسیم ستاره
رعایت تقسیم ستاره چه قدر مؤثر است؟
به چند دلیل ما باید در ترک کشی، تقسیم ستاره را رعایت کنیم. تقسیم ستاره ویژگی هایی دارد که گاهی نبودن این ویژگی ها باعث عملکرد بد مدار می شود. در این که چرا از تقسیم ستاره استفاده می کنیم چندین موضوع ممکن است دخیل باشند. ما به چند مورد از آنها می پردازیم.
تقسیم ستاره و بهبود توزیع جریان
یکی از موارد مهمی که در طراحی PCB باید رعایت شود، رسم ترک ها به گونه ای است که جریان کشی قطعات به راحتی امکان پذیر باشد. یعنی اگر قطعه ای بخواهد با جریان بالا کار کند، پهنای ترک طوری باشد که این جریان باعث اسیب به ترک نشود. اگر برای یک جریان بالا ترکی با پهنای کم در نطر بگیریم، هنگامی که قطعه جریان می کشد، ترک در اثر عبور جریان بالا و حرارت ایجاد شده، می سوزد و قطع می شود.
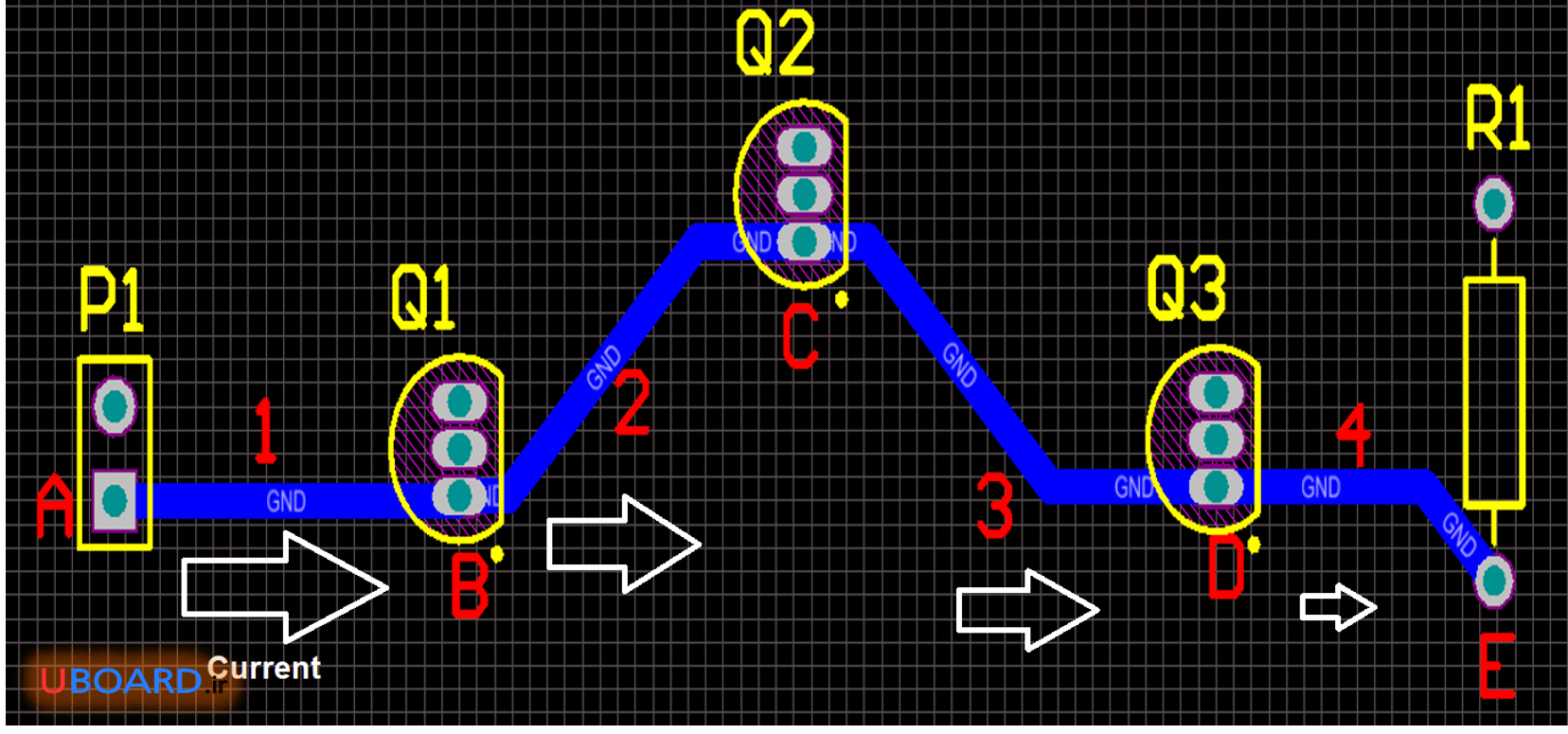
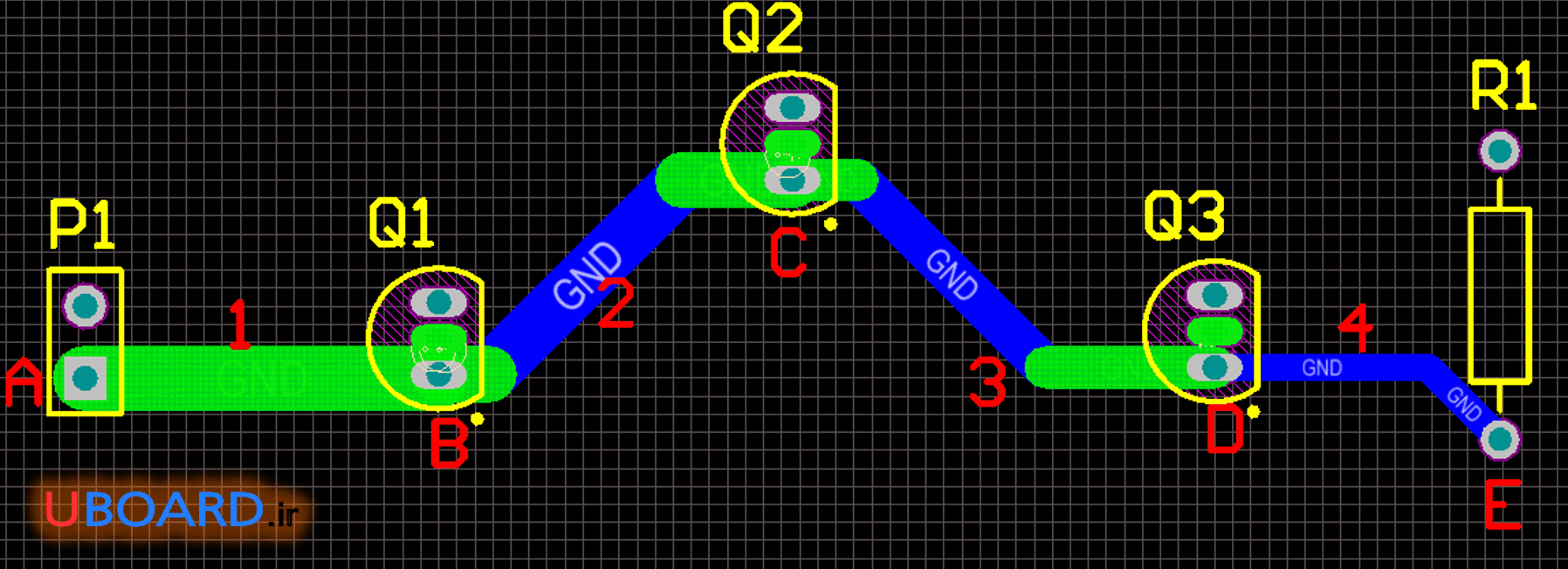
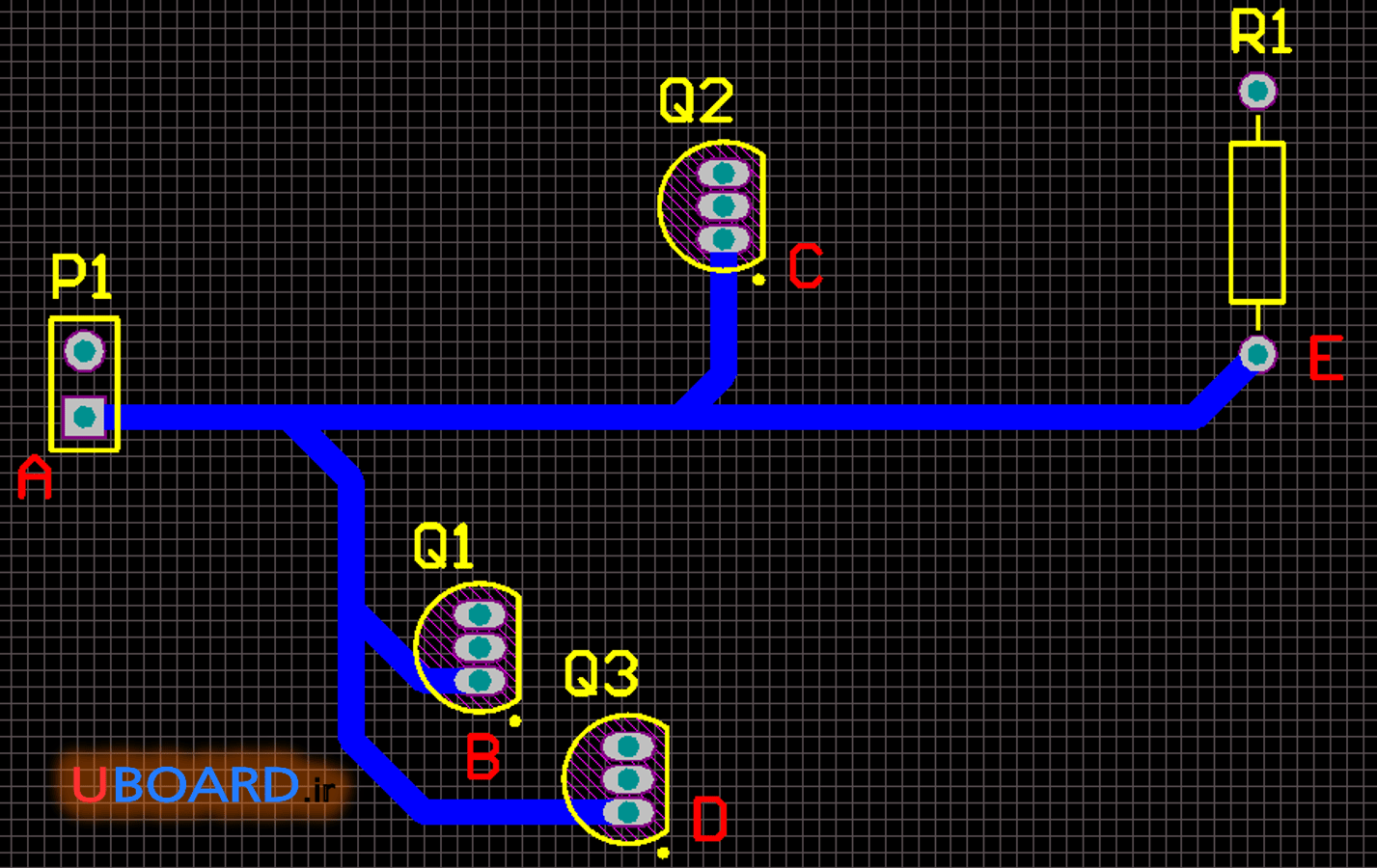
به تصور زیر دقت کنید. فرض کنید همۀ قطعات جریان بالایی می کشند. مجموع جریانی که قطعات می کشند روی ترک 1 می افتد. روی ترک 2، مجموع جریان سه قطعۀ بعدی، روی ترک 3، مجموع جریان دو قطعۀ بعدی و روی ترک 4 جریان قطعۀ آخر وجود دارد. در این طرح احتمال آسیب ترک 1 و حتی ترک 2 و 3 وجود دارد. زیرا از هر کدام از آنها جریان 2 الی 4 قطعه عبور می کند.
تصویر 3 – ترک کشی و توزیع نامناسب جریان
در قدم اول برای رفع این مشکل، پهن کردن ترک های 1 و 2 و 3 به نظر می رسد. اما پهن کردن ترک ها در این روش محدودیت دارد و ما نمی توانیم روی پد قطعات ترک پهن بکشیم. چون ترک به پدهای دیگر متصل و یا نزدیک می شود.
تصویر 4 – پهن کردن ترک ها به صورت ناصحیح
حال اگر از تقسیم ستاره استفاده کنیم این پهن کردن ترک ها به راحتی انجام می شود. در تصویر زیر دو روش پهن کردن ترک را می بینیم. در روش بالا یک ترک پهن وجود دارد که هر یک از المان ها با یک ترک متناسب با جریان خود به آن متصل شده اند. در روش پایین نیز تنها در بخش هایی که لازم بوده ترک پهن رسم شده. یعنی بسته به جریان عبوری از ترک پهنای آن متفاوت است.
تصویر 5 – پهن کرن ترک ها در تقسیم ستاره
تقسیم ستاره و بهبود فضای ترک کشی
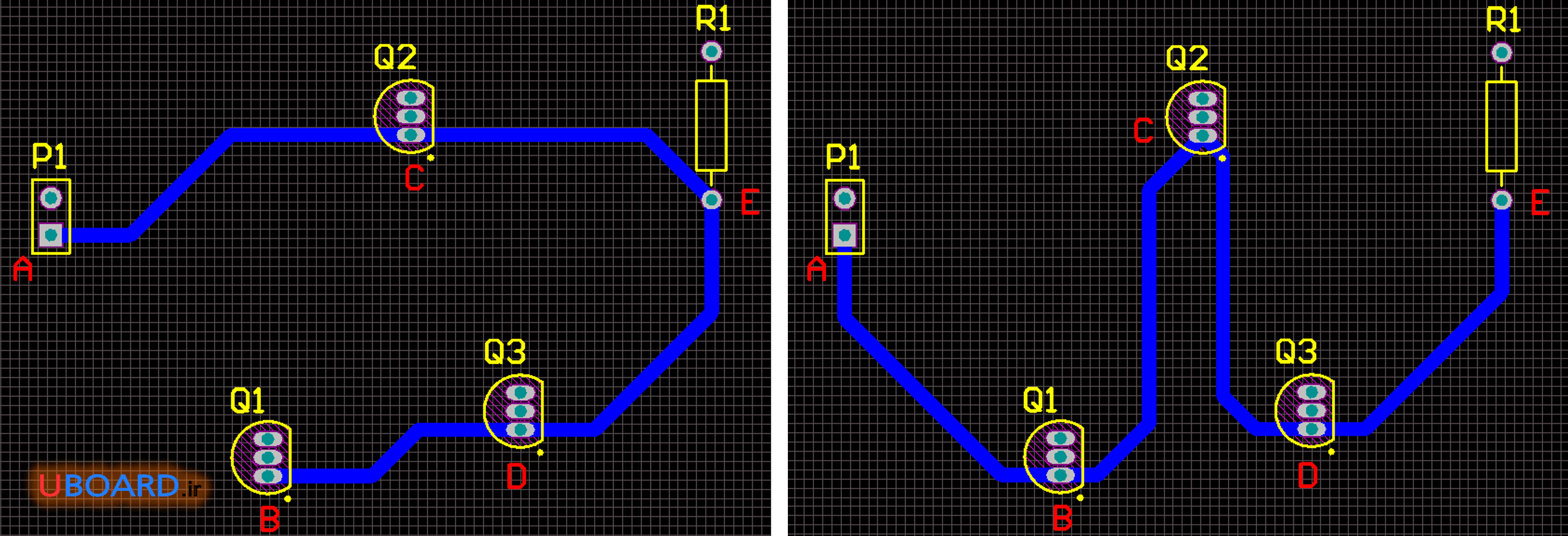
توزیع قطعات روی بورد در ترک کشی تأثیر چشمگیری دارد. در تصاویر بالا قطعات تقریباً به صورت افقی قرار داشتند و اگر هم از تقسیم ستاره استفاده نمی شد، فضای بورد حتی کمتر از حالت تقسیم ستاره هم اشغال می شد. اما گر توزیع قطعات طوری باشد که بخواهیم ترک مورد نظر را بدون تقسیم ستاره رسم کنیم، فضای بورد با ترک طوری اشغال می شود که رسم ترک های دیگر بورد را با مشکل مواجه می کند و فضا برای رسم ترک های دیگر اشغال می شود. به تصویر زیر توجه کنید.
تصویر 6 – رسم ترک برای قطعات با توزیع بالا و پایین
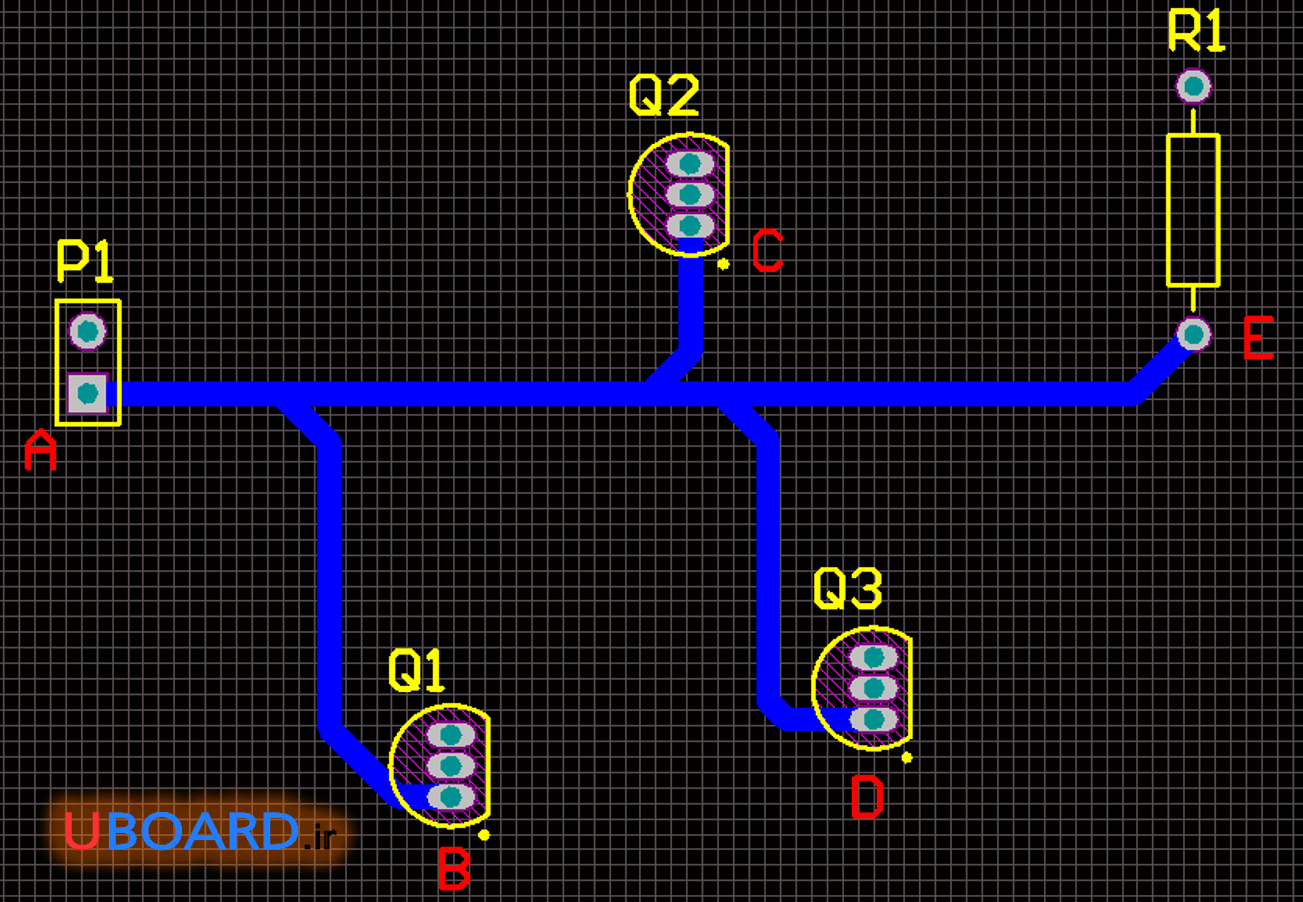
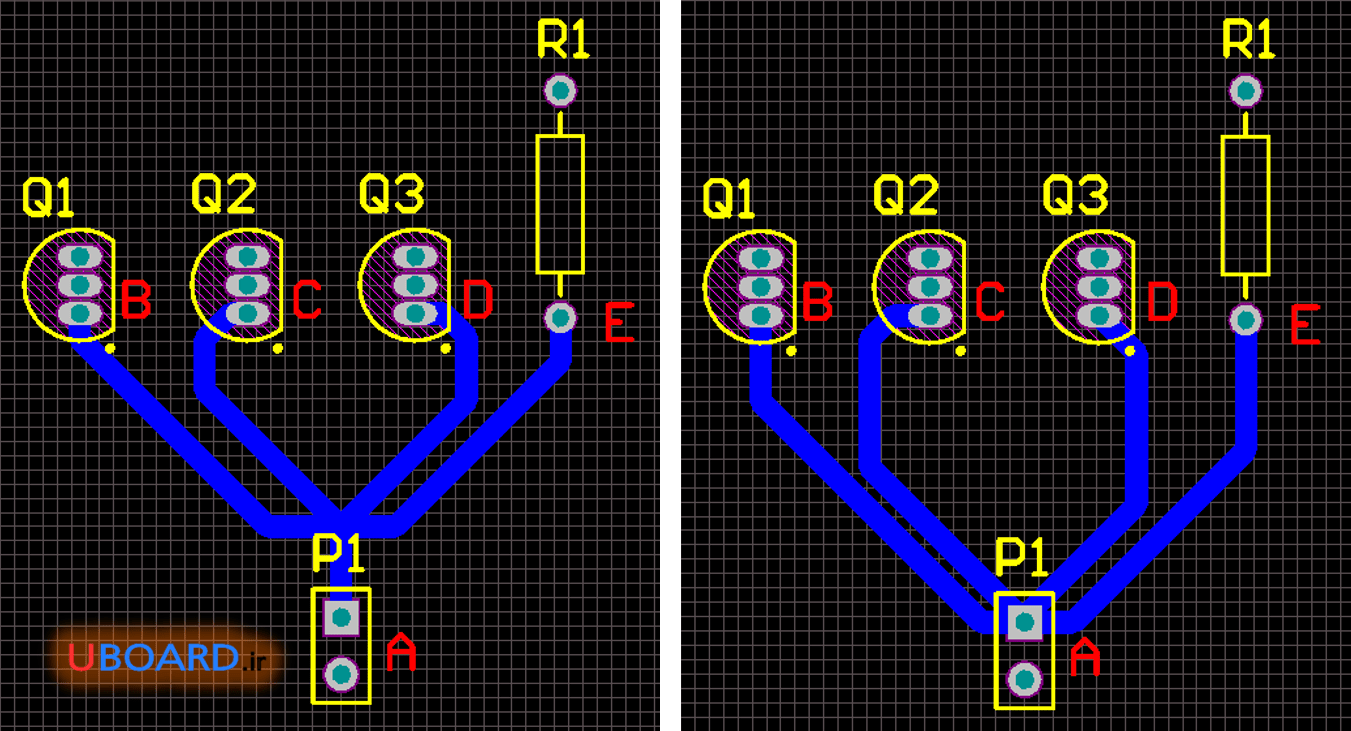
در هر دوی این روش ها ترک کشی نامناسب است. چرا که فضای زیادی از بورد به ترک مورد نظر اختصاص یافته است. با توجه به این که در PCBها ترک هایی که لازم است تقریباً به تمام قطعات متصل شوند، اغلب ترک های زمین و تغذیه هستند، همواره فضای زیادی از بورد به این ترک ها اختصاص می یابد. این موضوع زمانی چشمگیر است که تعداد قطعات زیاد باشد. در تصویر زیر تقسیم ستاره را می بینیم.
تصویر 7 – تقسیم ستاره برای قطعات با توزیع بالا و پایین
تقسیم ستاره اگر به درستی انجام شود، در هر نوع طرح با انواع توزیع قطعات، مفید است. در برخی از PCBها توزیع قطعات به گونه ای است که اگر از تقسیم ستاره استفاده نشود، امکان رسم برخی ترک های دیگر وجود ندارد.
تصویر 8 – تقسیم ستاره برای قطعات با توزیع بالا و پایین
تقسیم ستاره و امپدانس مسیر
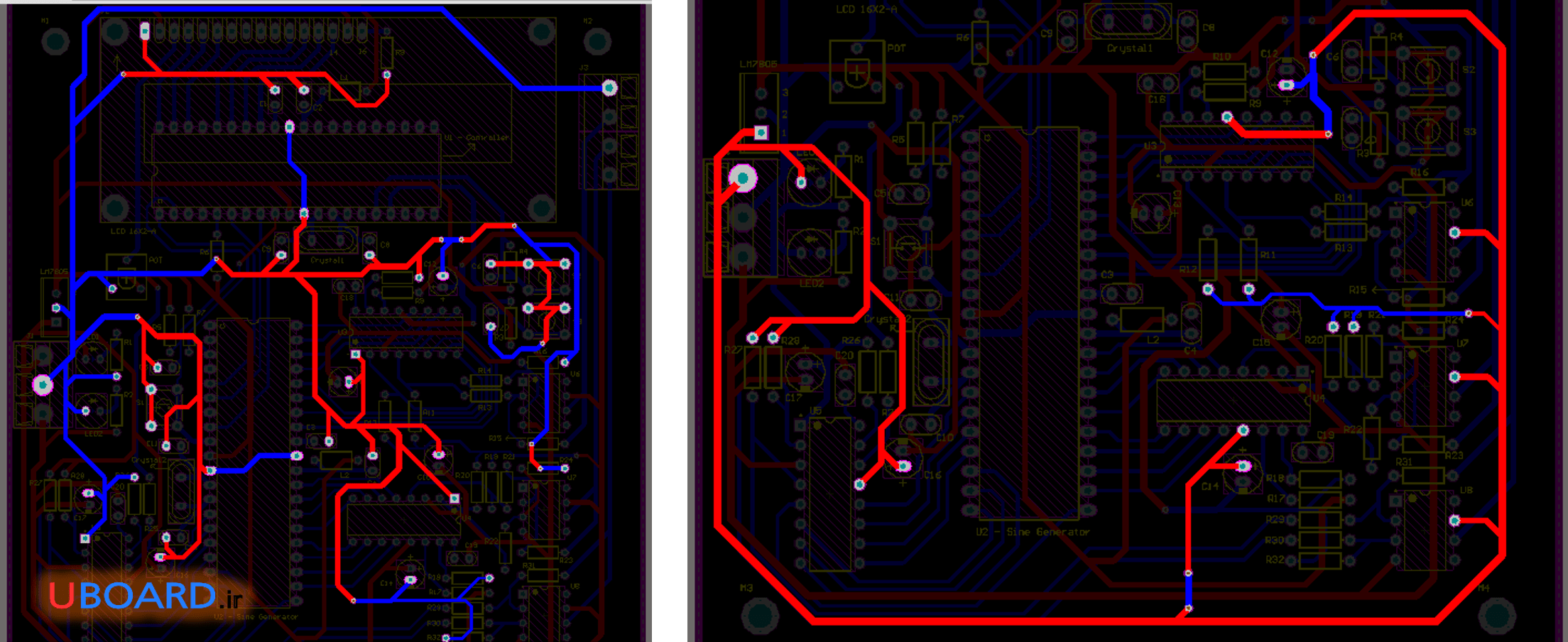
در ترک های طولانی همواره یک امپدانس وجود دارد که باعث افت ولتاژ دو سر ترک می شود. در تقسیم ستاره اگر به صورت صحیح آن را رسم کنیم، مقدار امپدانس مسیر کمتر می شود. برای کم شدن امپدانس مسیر بهتر است ترکی که از آن انشعاب گرفته می شود تا حد امکان پهن باشد. به ویژه برای خطوط زمین و تغذیه این نکته حتماً باید رعایت شود. به تصویر زیر توجه کنید. سمت چپ ترک های گراند و سمت راست ترک های VCC این بورد هستند.
تصویر 9 – ترک VCC و گراند در یک بورد نمونه
یکی از راه های کاهش امپدانس مسیر استفاده از پولیگان (polygon) است. در نرم افزار آلتیوم ابزار رسم پولیگان وجود دارد. با این ابزار یک لایۀ مسی در فضاهای خالی PCB قرار می گیرد. این لایه ممکن است به زمین متصل شود. که اگر به زمین متصل شود، با توجه به این که پهنای مسیر ترک زمین زیاد می شود، امپدانس مسیر آن کم می شود. در تصویر زیر در لایۀ بالا (سمت راست تصویر) پولیگان به زمین و در لایۀ پایین (سمت چپ تصویر) پولیگان به VCC متصل شده است.
تصویر 10 – استفاده از پولیگان برای کاهش امپدانس مسیر
در تصویر زیر نیز با استفاده از ابزارهای fill و solid region در آلتیوم، مسیرهای گراند (سمت راست) و VCC (سمت چپ) پهن شده اند.
تصویر 11 – پهن کردن مسیرهای زمین و تغذیه با ابزارهای fill و solid region
امپدانس مسیر به ویژه در مدارات فرکانس بالا دارای اهمیت است. برای طراحی مدارات فرکانس بالا نکات زیادی وجود دارد. مثلاٌ یک نکته این است که طول مسیر زمین و تغذیه برای تقویت کننده های چند طبقۀ فرکانس بالا باید با هم برابر باشد. فرض کنید تصویر زیر یک مدار فرکانس بالاست. به دو روش تقسیم ستاره برای رساندن ترک زمین به این المان ها توجه کنید. در هر دو روش انشعاب از یک نقطه گرفته شده و همچنین طول ترک ها برای هر یک از قطعات یکسان است.
تصویر 12 – تقسیم ستاره برای ترک زمین در چند طبقه تقویت کنندۀ فرکانس بالا
تقسیم ستاره برای VCC و گراند آی سی ها
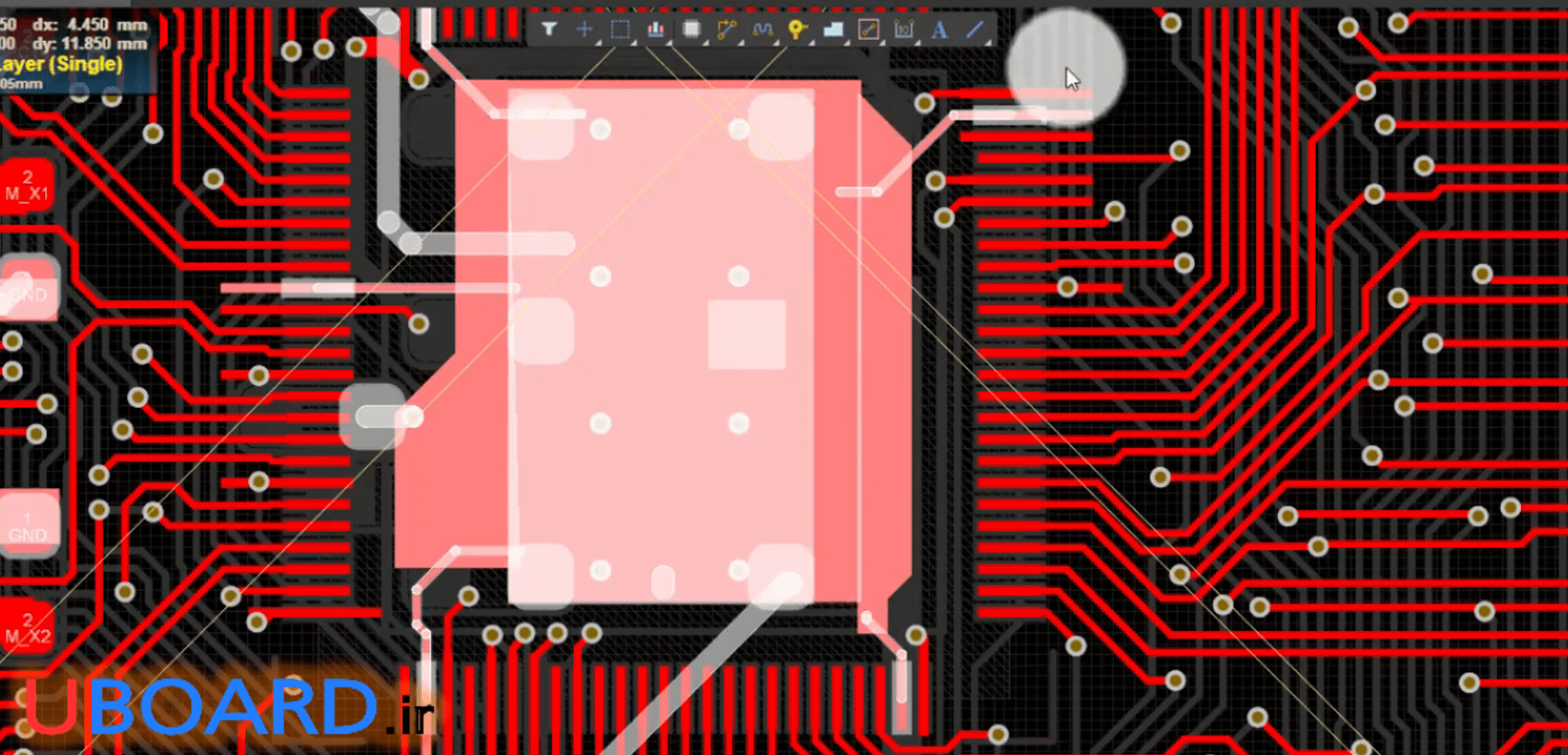
برای رساندن زمین و تغذیه به آی سی هایی که چند پایۀ VCC و گراند دارند، یک روش این است که ترک های گراند و تغذیه را به زیر آی سی منتقل کنیم و هر پایه های که قرار بود به زمین و VCC وصل شود، از زیر آی سی انشعاب گرفته شود. در تصویر زیر بخشی از PCB بورد توسعۀ STM32F10xVxxx را مشاهده می کنید. یک پولیگان در زیر آی سی و در لایۀ بالا ترسیم شده و این پولیگان، زمین مدار است. برای پایه های گراند آی سی از آن انشعاب گرفته شده است.
تصویر 13 – انشعاب زمین برای پایه های میکروکنترلر
این پولیگان با وایا به پولیگان لایۀ زیر متصل است و پولیگان زیر بورد نیز به زمین مدار وصل می باشد.
تقسیم ستاره و اهمیت آن
با توجه به مطالب گفته شده، درمی یابیم که در ترک کشی به ویژه ترک های زمین و تغذیه که قرار است به چندین نقطۀ مدار وصل شوند، حتماً از تقسیم ستاره استفاده کنیم. این موضوع به قدری اهمیت دارد که رعایت نکردن آن ممکن است باعث آسیب به ترک ها (در اثر جریان بالا) و عملکرد بد مدار (در اثر امپدانس مسیر و …) و یا کلاً کار نکردن مدار شود.
یکی از اصولی که ما رعایت می کنیم این است که به یک پد دو یا چند ترک متصل نشود. در تصویر 3 و 6 می بینیم که به پدهای B و C و D دو ترک متصل شده است. این موضوع در مونتاژ اهمیت دارد. اگر به هر دلیلی پد های B یا C و یا D آسیب ببینند و کنده شوند، مسیر برای همۀ قطعات بعد از آنها قطع می شود. و همچنین دو ترک قطع شده خواهیم داشت. اما مثلاً اگر در تصویر 5 و 7 هر کدام از پدهای B تا E آسیب ببینند، تنها اتصال همان نقطه قطع می شود. این موضوع خود باعث بیشتر شدن اهمیت تقسیم ستاره در PCB می شود.
در آموزش طراحی PCB موضوعات و نکات مختلف طراحی PCB مورد بحث قرار گرفته است. سر فصل های هر یک از این دوره ها در صفحۀ معرفی آن دوره بیان شده است. برای درک بهتر موضوع تقسیم ستاره، ویدئوی این نوشته را مشاهده بفرمایید.
از تقسیم ستاره در PCB نتایج زیر حاصل می شوند:
- تقسیم ستاره یک کار ساده اما مهم است. اهمیت تقسیم ستاره به قدری است که در صورت رعایت نکردن آن یا رعایت نکردن صحیح آن، ممکن است در عملکرد PCB ساخته شده مشکل به وجود بیاید یا PCB آسیب ببیند.
- تقسیم ستاره برای هر ترکی که قرار است به چند نقطه متصل شود باید رعایت شود.
- برای ترک های گراند و تغذیه چون به چند نقطه متصل می شوند حتماً باید از تقسیم ستاره استفاده کرد. همچنین پهنای ترک ها باید متناسب با جریانی که قرار است عبور دهند، در نظر گرفته شود.
- برای پهن شدن مسیرهای تغذیه و گراند می توان از پولیگان استفاده کرد.
- تقسیم ستاره باید به صورت صحیح رسم شود. به طوری که ترک های یک بورد همگی به مقصد برسند.
- در مدارات فرکانس بالا با توجه به امپدانس خطوط، اختلاف فاز سیگنال ها، موج برگشتی و … نکات خاصی برای طراحی PCB و تقسیم ستاره وجود دارد.
- در رساندن تغذیه و زمین به آی سی های دارای چند پایۀ تغذیه و زمین، استفاده از پولیگان زیر آی سی و انشعاب گرفتن از آن توصیه می شود.
آموزش های مرتبط با این نوشته:


















سلام و تشکر بابت نوشته و فیلم خوبتون. توی طراحی به یک مشکل برخوردم. من توی برد هم آنالوگ دارم هم دیجیتال دارم. میتونم که یک خط ذخیم از Vcc بکشم و ببرم نزدیک قسمت های آنالوگ و دیجیتال و یک انشعاب بهشون بدم. میتونمم که از همون ورودی تغذیه مسیر رو به دو قسمت تقسیم کنم و کلا از همون ورودی تغذیه جدا کنم. نظرتون شما در این مورد چیه؟ البته اگر بخوام که مستقیم از ورودی تغذیه ها رو جدا کنم کار خیلی سخت میشه من بردم پیچیده و شلوغه و فکرنکنم برای این کار جا باشه.
سلام. خواهش میکنم. لطف دارید. توی روش اول اگه بخواید VCC و گراند رو به تغذیه و گراند المان های آنالوگ برسونید میشه با فریت بید یا سلف و خازن روی مسیر تغذیۀ دیجیتال، برای المان های آنالوگ تغذیه و گراند گرفت. که با توجه به جریان کشی قطعات آنالوگ و تعداد اونا و … روش های مختلف داره و خارج از حیطۀ یه نوشته س. روش دوم یه روش خوبه. یعنی شما از همون ابتدای گرفتن تغذیه از پایۀ کانکتور (حالا یا جک آداپتور یا هر پین دیگه ای که ورودی تغذیه س)، دو تا ترک جدا رسم کنید. یکی برای تغذیۀ آنالوگ و یکی هم برای تغذیۀ دیجیتال. که البته این مورد هم ممکنه باعث بشه بردتون بزرگتر بشه یا بخواید تعداد لایه هاتونو بیشتر کنید. حالا یه نکتۀ جالب رو خدمتتون بگم. میشه با استفاده از تعریف یه قطعه با توجه به مطالب بخش «تایپ Net Tie (in BOM) در کتابخانۀ شماتیک» نوشتۀ «بررسی پنجرۀ Properties در کتابخانه شماتیک نرم افزار Altium Designer»، به ترک آنالوگ و دیجیتال اسم های جدا داد. درصورتی که به هم متصل اند. مثلاً اسم Net اونا رو گذاشت: AVCC و DVCC.
سلام. اگر توی ابعاد کم برد نتونیم تقسیم ستاره رو رعایت کنیم و از طرفی نخوایم برد رو چند لایه کنیم و همچنین برد رو بزرگتر کنیم، راهی هست که ذخامت خطوط تغذیه و همچنین تقسیم ستاره رو رعایت کنیم؟
سلام. به هر حال باید یکی از محدودیت ها رو کنار بذارید. یا با تعداد لایه های بیشتر و یا با ابعاد بیشتر برد، امکان رعایت تقسیم ستاره رو فراهم کنید. البته چه فضا کم باشه و چه زیاد، به هر حال باید اتصال برقرار بشه و رسم ترک بدون رعایت تقسیم ستاره هم فضایی رو اشغال میکنه. توی چنین مواردی جایگذاری مناسب قطعات خیلی مهمه و میتونه به امکان رعایت تقسیم ستاره تو رسم مسیرها کمک کنه. بعضی مواقع هم برای کم کردن امپدانس ترک هایی که جریان بیشتری روی اوناس روی ترک لحیم کاری می کنن. بعضی اوقات هم از جامپر استفاده می کنن و نقاطی از برد رو با سیم به هم متصل می کنن.